I. Introduction
Collapsing oil prices since 2014 have converted the landscape of budget surpluses into deficits in many Gulf Cooperation Council (GCC) states. Consequently, these countries have started to run down their sovereign funds’ reserves and raise funds globally to finance planned public spending and investments. The aggregate primary issuance of bonds and Sukuk has increased from $36 billion in 2014 to approximately $635 billion in 2022.
The COVID-19 pandemic has brought global economies to a standstill and caused oil prices to crash. Oil price uncertainty, together with fiscal pressures, are among the most decisive forces that may influence sovereign default risks and sovereign credit ratings of the GCC countries and, thereby, their cost of access to external financing. This study empirically examines the effect of oil price uncertainty (proxied by the conditional variance of the oil price change forecast error) on the sovereign default risk of the GCC states. This study is crucial for policy making and public debt management in the GCC states. Additionally, studying the effects of oil price uncertainty provides new knowledge about how investors should consider oil price uncertainty when pricing the government debt of oil-producing countries such as the GCC states.
Even though the effect of oil prices on GCC sovereign credit risk (approximated by the sovereign credit default swap spreads, Credit Default Swap (CDS)) has been previously examined (Hammoudeh et al., 2013; Naifar et al., 2020; Shahzad et al., 2017), this study is distinguishable as it focuses on how uncertainty resulting from oil price volatility affects sovereign credit risk.[1],[2] Most importantly, unlike previous studies, this study considers how sovereign credit risk asymmetrically responds to oil price uncertainty.[3] Additionally, this study aims to assess the impact of oil market uncertainty after adjusting the data for outliers caused by exogenous extreme oil shocks.
To accomplish the objectives of our study, we implemented a structural vector autoregression with multivariate GARCH-in-mean (VAR-GARCH-in mean) framework proposed by Elder (2021). In this framework, uncertainty is simultaneously determined by an integrated GARCH-in-mean process. Specifically, this method is a dynamic structural system consisting of a linear function of the variables namely CDS spreads and change in oil prices augmented by a conditional variance of oil prices that affects the conditional mean. In contrast to two-stage methods, this novel framework estimates all parameters concurrently, resulting in internally consistent reliability estimates that avoid the “generated regressor” issue in the second-stage estimation (e.g., Maghyereh et al., 2019).
II. Methodology and data
Following Elder (2021), the VAR for the conditional mean can be specified as follows:
Byt=C+A1yt−1+A2yt−2+…+Asyt−s+Λ(L)H12t+εt for 1≤t≤T,
where is a vector of monthly log-returns of sovereign CDS spreads and the monthly log-returns of oil prices, is a diagonal conditional covariance matrix that we assume follows a bivariate version of the GARCH model, is a lag operator polynomial matrix, denotes the data set at time and is the lag order.[4] In this specification, the matrix is used to measure the conditional volatility of oil prices, which allows for testing the oil price uncertainty shocks on the conditional mean of CDS spreads
We identify constraints in structural shocks by assuming that concurrent disturbances are uncorrelated. Consequently, the covariance matrix, becomes diagonal, and its structural variance function can reduce to the following form:
\small diag\left( H_{t} \right) = C_{v} + \sum_{i = 1}^{q}{F_{i}{diag(\eta}_{t - i}\grave{) + \sum_{j = 1}^{r}{G_{j}{diag(h}_{t - j})}}} \tag{2}
where are the parameter matrices with being diagonal to ensure positive definiteness of The FIML method is used to estimate both of the aforementioned equations simultaneously.
To analyze the potential asymmetrical responses of CDS spreads to unexpected oil price shocks, we carried out the impulse response functions (IRFs). The Bayesian Monte Carlo simulation with replications was used to construct the confidence intervals for IRFs.
We used monthly data on the sovereign CDS spreads with a 5-year maturity. The sample covered the period from 2011:05 to 2022:05.[5] Our sample consisted of four GCC states, namely Bahrain, Qatar, the United Arab Emirates (UAE), and Saudi Arabia. As a proxy for the global oil benchmark, we used Brent crude oil prices. All data were derived from Thomson Reuters’ Datastream.
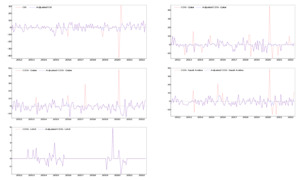
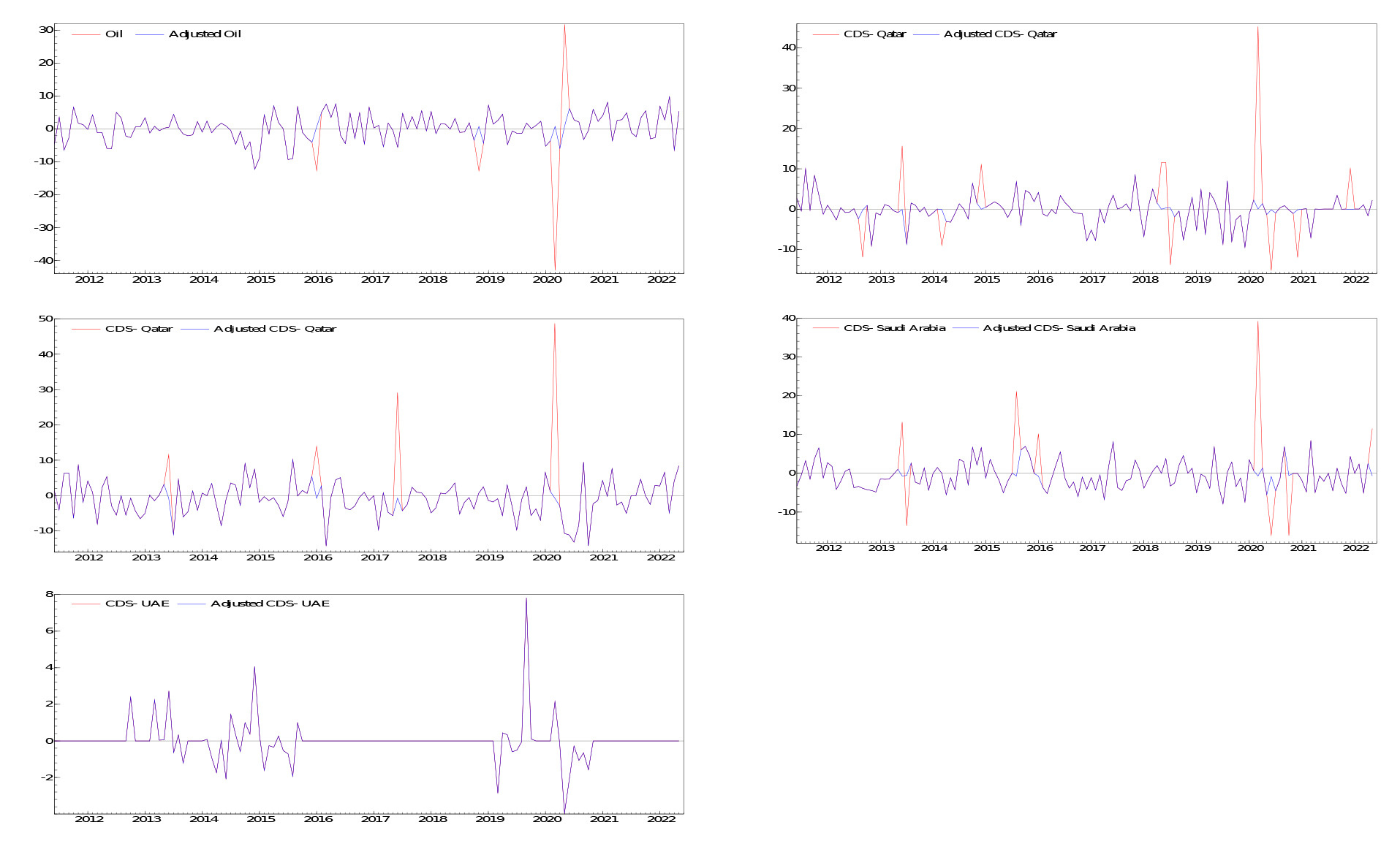
According to Charles et al. (2020), failure to correct for outliers in oil volatility that are caused by exogenous events (resulting from political conflict, natural disasters, or wars) can lead to a bias in parameter estimates of the dynamics and consequently misrepresent the impact of oil shocks through the analyses of the IRF. Therefore, it is necessary to first detect the existence of outliers within our data set and subsequently adjust for these outliers. We detected the outliers using the Laurent et al. (2016) test based on Monte Carlo simulations. We then filtered out these detected outliers from the observed return series as follows:
{\widetilde{r}}_{t} = r_{t}^{*} - \left( r_{t}^{*} - {\widetilde{\mu}}_{t} \right){\widetilde{I}}_{t}\tag{3}
where is the adjusted return series, is the conditional mean of from the ARMA(p,q)–GARCH(1, 1) process, and is a binary variable with a value of if day witnesses an outlier and if otherwise. Figure 1 shows that the size of these additive outliers is large, especially in the cases of Qatar and Saudi Arabia. Adjusting for the outliers appears to produce an incremental effect on the dataset during the oil crash following the COVID-19 pandemic.
III. Results
The coefficient estimates in the conditional volatility function are reported in Table 1. The estimates show that the ARCH and GARCH coefficients were significant in the CDS spread equation in all cases. In the crude oil equation, the ARCH coefficients were also significant. These findings suggest that the volatility processes underlying changes in CDS spreads and oil prices are persistent, thus validating our model. In addition, the only significant lagged squared errors coefficient (ARCH term) in the oil volatility equation indicates relatively and persistently weak oil volatility.[6]
Table 2 reports the point estimates of the coefficient Across all countries, the table shows a positive and significant The values of the coefficients for Bahrain, Qatar, Saudi Arabia, and the UAE are 0.204, 0.164, 0.170, and 0.059, respectively. These findings suggest that higher levels of conditional oil volatility have a short-term tendency to increase CDS spreads. These findings contradict those of Naifar et al. (2020), who provide evidence of no statistically significant connection between oil uncertainty and the CDS. Table 2 also shows that the responses to oil volatility shocks are the highest in Bahrain and Saudi Arabia. The high rates can be attributed to the significance of oil in financing government revenues in both nations. Another explanation stems from the role of oil uncertainty in exaggerating the risk ratings (Liu et al., 2016) of oil-exporting nations. This argument suggests an increase in the CDS spread following the high fluctuations in oil prices.
To render an explicit economic interpretation of our results, we multiplied the average shock magnitude (16.698) with the coefficient [7] An increase in oil price uncertainty by one standard deviation tends to increase the percentage change in CDS spreads within one month by approximately 3.406%, 2.738%, 2.839%, and 0.985% in Bahrain, Qatar, Saudi Arabia, and the UAE, respectively. These findings indicate that oil price uncertainty has a significant impact on the sovereign creditworthiness of the GCC bloc. However, we notice that the positive impact of oil price uncertainty on the CDS spreads of the UAE is weaker and less persistent than that of other GCC countries. This could be explained by the high level of economic diversification in the UAE. According to the World Bank (2022), hydrocarbons account for 36% of total revenue for UAE compared with 81%, 82%, and 68% for Bahrain, Qatar, and Saudi Arabia, respectively.
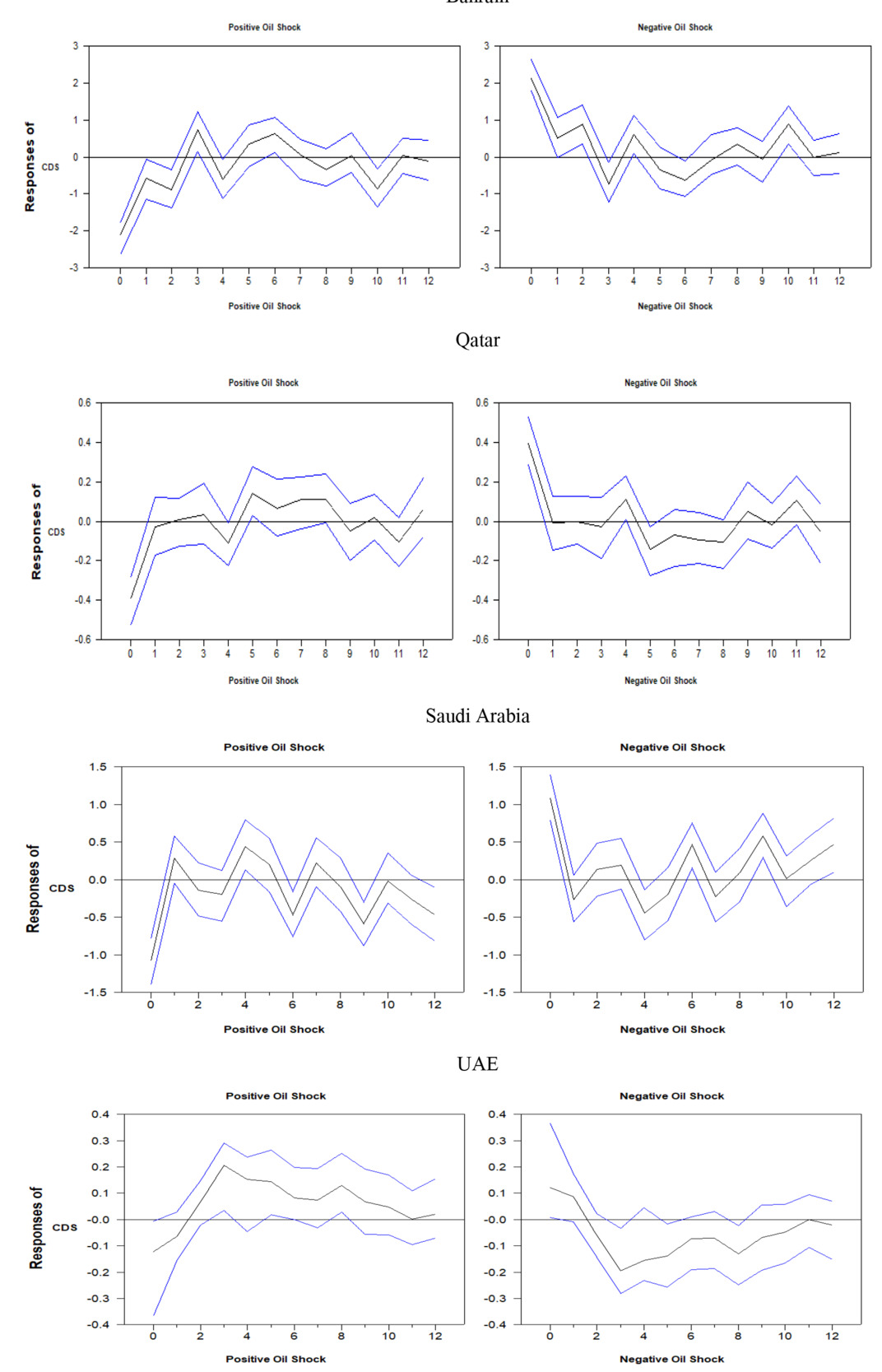
For further understanding of the dynamic impact of oil shocks on sovereign credit risk with the presence of uncertainty, we estimated the asymmetric IRFs over a 12-month period. The first column of Figure 2 displays the response of CDS spreads to a positive oil price shock. The 95% confidence intervals are represented by blue lines.[8] Noticeably, the reaction depends on the sign of shock, with that being negative up to one lag with the positive oil shocks. While the observation holds for all sampled GCC nations, it is less evident in the UAE. A quick comparison between the four countries reveals a stronger impact of positive shocks on the CDS spread in Saudi Arabia. Conversely, the UAE’s sovereign risk is the least affected by positive innovations. It was also observed that the reaction to positive shocks reaches its maximum after the first quarter in both Saudi Arabia and the UAE. The influence of negative shocks, in the second column of Figure 2, produced a reversed result. That is, the impact of shocks is positive at the first lag, indicating that negative oil shocks have a tendency to increase spreads almost immediately after they occur. These results confirm the asymmetric impact of oil shocks on CDS spreads. These findings are consistent with early findings that different oil shocks have asymmetric impacts on the real GDP of oil-exporting countries (e.g., Elder, 2021; Yildirim & Arifli, 2021). This, in turn, is expected to heterogeneously pass on sovereign risk in the GCC countries.
IV. Conclusion
We examined the effect of oil price uncertainty on sovereign credit risks in four oil-producing countries. We found a positive impact of oil uncertainty on CDS spreads, implying that higher oil volatility leads to an increase in the sovereign default risk of GCC states. This outcome implies that oil uncertainty exerts a more profound impact on credit risk in less diversified economies. However, contrary to previous studies, we document that oil price shocks have asymmetric effects on the sovereign CDS spreads.
Regarding policy making, our findings suggest that the impact of some sudden shocks in oil prices might be long-lasting, requiring immediate intervention to manage the cost and timing of borrowing. Others, however, might disappear in the short-run; thus, taking some decisions against them can be catastrophic. The outcome of the policymaker’s behavior may result in downgrading the credit rating of countries that take aggressive decisions at an inappropriate time. Our findings also call for economic diversification by the GCC countries to ensure their solvency when exposed to fluctuations in oil prices.
CDS spreads reflect the perception of international investors about the financial situation of debtor countries, thereby their risk of sovereign credit.
Volatility can be considered as one of the underlying sources of uncertainty in financial markets. Volatility measures the variation in a financial variable, and it can be caused by many factors, including market sentiments and geopolitical events. Market participants may view the future as uncertain and be less confident in their price predictions when market volatility is high.
The fact that fiscal policy in oil-exporting countries is pro-cyclical rather than countercyclical lends credence to the possibility of asymmetric effects of oil shocks on credit market assessments of the creditworthiness of these countries.
Our results are robust to other alternative lag lengths (i.e.,
The sample countries and the time frame were selected based on data availability.
These findings are consistent with earlier studies (see Elder, 2021; Elder & Serletis, 2010).
The average shock magnitude is calculated using the sample standard deviation of the conditional volatility of the oil prices.
We use Monte Carlo simulations with 1000 replications.