Does Climate Finance Mitigate Energy Uncertainty in Europe?

I. Introduction

In recent times, energy uncertainty has become a significant issue confronting Europe. The uncertainties in energy supply have intensified due to global crises such as the Russia-Ukraine conflict. Additionally, Europe is phasing out nuclear energy stations to address climate change concerns. However, this policy is exacerbating energy problems and leading to increased costs of energy sources. Consequently, Europe must identify solutions that simultaneously address energy issues and combat climate change.

The literature increasingly focuses on examining the impact of climate finance on factors related to energy. Njangang et al. (2024) investigate the effects of climate finance on energy vulnerability during the period 2000-2019 for 74 developing countries, finding that climate finance reduces energy vulnerability. Zhao et al. (2024) examine the influence of climate finance on renewable energy development for 63 countries from 2000 to 2019, concluding that climate finance promotes renewable energy development. Aquilas and Atemnkeng (2022) study the significance of climate finance in the Congo Basin from 2002 to 2020, revealing that increased climate finance accelerates the transition to renewable energy. Qi et al. (2023) also highlight the importance of green finance projects for advancing renewable energy. Furthermore, Tang and Zhou (2023) assess the impact of climate finance on renewable energy development in China, indicating that climate finance is crucial for local and neighboring countries’ renewable energy progress. Briera and Lefèvre (2024) show that climate finance helps mitigate the capital costs of renewable energy investments, thereby reducing uncertainties.

The literature clearly demonstrates that climate finance alleviates energy-related vulnerabilities and uncertainties while fostering renewable energy development. Enhancing climate finance not only benefits environmental quality but also reduces energy-related uncertainties. Despite this, there is a gap in the literature regarding the exploration of climate finance’s influence on novel energy variables such as energy uncertainty, even though a theoretical linkage exists.

Addressing both energy uncertainty and climate change is currently a priority for the European region. This research empirically evaluates the impact of climate finance on energy uncertainty in Europe. The study contributes to the existing literature in two significant ways. Firstly, it employs a novel variable, energy uncertainty, recently developed by Dang et al. (2023). Although some studies (Işık et al., 2024; Kocourková et al., 2024) have utilized the energy uncertainty variable, its relationship with climate finance has not yet been examined. Secondly, the issues tackled in this work align with the European region’s energy and climate policies.

The structure of this paper is as follows: Section II defines the data and outlines the methodology; Section III presents the empirical estimations; and Section IV concludes.

II. Data and Methodology

A. Data

To examine the relationship between energy uncertainty, climate finance, economic development, and government effectiveness, an analysis was conducted for 11 European countries: Belgium, Croatia, Denmark, France, Germany, Greece, Ireland, Italy, Netherlands, Spain, and Sweden, based on the availability of energy uncertainty data from 2001 to 2019.

Energy uncertainty (EU) serves as the dependent variable, measured by an index, while climate finance (CLF) is the independent variable, expressed as a percentage of GDP. Economic development (PGDP), measured in US dollars per capita, and government effectiveness (GEF), assessed via an index, function as control variables in this analysis. All data utilized are annual figures.

Data on energy uncertainty were sourced from the Economic Policy Uncertainty web portal, climate finance data were obtained from OECD Data Explorer, and economic development and government effectiveness data were retrieved from World Bank Data.

Logarithmic transformations were applied to the energy uncertainty and per capita GDP data, referred to as LOGEU and LOGPGDP respectively.

B. Methodology

B.I. Method of moments quantile regression

The assumption of ordinary least squares (OLS) based on mean value and normal distribution can be distorted due to fluctuations in economic data. This heteroscedasticity may arise from financial and geopolitical instabilities, wars, pandemics, disasters, and other uncertainties. Particularly, the CLF and energy systems are impacted by such occurrences. To address the heteroscedastic nature of the data, the methods of moments quantile regression (MMQR) is employed. Borojo et al. (2024) also utilized the MMQR approach to investigate the heterogeneous effect of CLF on energy efficiency. A key advantage of the MMQR method is its ability to efficiently analyze the impact of regressors across different quantiles of the response variable. The MMQR approach, as demonstrated by Machado and Silva (2019), is shown in Equation (1).

$${LOGEU}_{it} = \alpha_{i} + X_{it}' \beta +(\delta_{i} + Z_{it}' \gamma) U_{it} \tag{1}$$

In Equation (1), $X_{it}'$ includes the right-hand side variables’ matrix, specifically, $X_{it}' = \lbrack{CLF}_{it}\ \ {LOGPGDP}_{it}\ {GEF}_{it}\rbrack'$, and β denotes the vector containing those variables’ coefficients. $\alpha_{i}$ represents the individual fixed effect whereas $\delta_{i}$ expresses the specific quantile fixed effect for i^th country. Z_it stands for the known differentiable transformations’ vector related to the independent factors, which satisfy the probability of $P\left\{ \delta_{i} + Z_{it}' \gamma > 0 \right\} = 1$. $U_{it}$ indicates a random variable independent of $X_{it}$ which is not observed, normalized for the satisfaction of the moment condition such as ${E(U}_{it}) = 0,\ E(\left| U_{it} \right|) = 1$.

Applying the above-mentioned references and considering the exogenous nature of the independent factors, the first moment conditions are estimated to obtain the estimated coefficients of $\alpha_{i}$, $\beta'$, $\delta_{i}$, $\gamma'$ and $q(\tau)'$ (see Machado & Silva, 2019). Consequently, Equation (1) can be expressed in the conditional quantile as follows:

$${Q}_{Y}\left( \tau\left| X_{it} \right.\ \right) = \left( \alpha_{i} + \delta_{i}q(\tau) \right) + X_{it}' \beta + Z_{it}' \gamma q(\tau)\tag{2}$$

B.II. Partially linear functional-coefficient panel model

While the MMQR method addresses the issue of heterogeneity, it still assumes linearity. The relationship between energy uncertainty and climate finance may also be non-linear. Specifically, economic fluctuations can impede climate investments, and these fluctuations are unpredictable, leading to non-linearity. Therefore, the effects of CLF on LOGEU depend on LOGPGDP. To address both non-linearity and heterogeneity, this study employs the partially linear functional-coefficient panel data model developed by Zhang and Zhou (2021). The model is generally represented as follows:

$$\begin{aligned} {LOGEU}_{it} &= \varphi_{0} + G\left( {LOGPGDP}_{it} \right){CLF}_{it}\\ & \quad + \varphi_{1}{LOGPGDP}_{it} + \varphi_{2}{LOGPGDP}_{it}\\ & \quad + u_{i} + \varepsilon_{it} \end{aligned}\tag{3}$$

where $G\left( {LOGPGDP}_{it} \right)$ is an unknown coefficient of the function evaluating the marginal effect of ${CLF}_{it}$ on ${LOGEU}_{it}$.

III. Empirical Findings

A. Preliminary analysis

The initial step involves conducting the CD test (Pesaran, 2004). As indicated in Table 1, the p-values of all tests are statistically significant at the 1% level, confirming cross-sectional dependence within the regression model’s residuals based on the variables used.

Given the presence of cross-sectional dependence, second-generation methods are required. Consequently, the CIPS unit root test (Pesaran, 2007) was conducted to verify the stationarity of the variables. The results, as presented in Table 1, indicate that all examined variables are integrated at first differences, with p-values demonstrating statistical significance at the 1% level.

Cross-sectional dependence confirms the need for Westerlund’s (2007) cointegration test. The results indicate a long-term relationship among the factors, with all p-values being statistically significant.

B. Baseline results

The findings presented in Table 2 indicate that climate finance has a negative influence on LOGEU in Europe according to the POLS model. Additionally, LOGPGDP positively affects LOGEU, whereas GEF has a negative impact. Notably, the negative effect of CLF on LOGEU is consistent across both fixed effects and random effects estimations.

Furthermore, the impact of CLF on LOGEU is assessed across various quantiles of LOGEU (Table 3). The analysis reveals that CLF has a negative and significant effect on LOGEU at lower and median quantiles: 5%, 15%, 25%, 35%, 45%, 55%, and 65%. Moreover, these findings are consistent with those reported by Borojo et al. (2024), but contrast with the results of Njangang et al. (2024), who observed a significant effect in higher quantiles. Overall, the results further validate the research hypothesis, theory, and baseline results presented in Table 2, despite the lack of effect in higher quantiles. The absence of CLF’s effect on higher quantiles of LOGEU supports the non-linearity assumption.

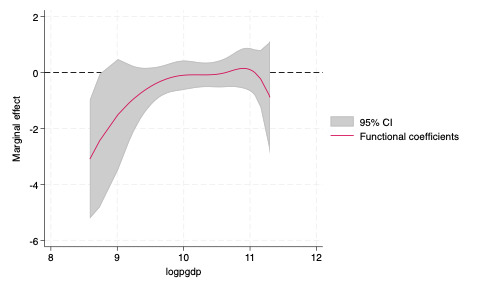
Due to the assumption of non-linearity, a PLFC panel data model is used to examine the impact of CLF on LOGEU. CLF includes a function that incorporates LOGPGDP (Figure 1). The results indicate that the effect of CLF on LOGEU can be both positive and negative. Specifically, the marginal effect of CLF on LOGEU is negative when LOGPGDP ranges from 8.587% to 10.637%. The effect becomes positive between growth rates of 10.639% and 11.047%, and turns negative again between growth rates of 11.071% and 11.300%. These findings imply that an average level of LOGPGDP moderates the effect of CLF on LOGEU.

Figure 1.Climate finance’s marginal effect on energy uncertainty

Note: This plot shows the non-parametric effect of CLF on LOGEUI, using LOGPGDP in the function of CLF.

IV. CONCLUSION

This study investigates the impact of CLF on LOGEU in Europe. The linear results from the MMQR method indicate that CLF reduces LOGEU across quantiles ranging from 5% to 65%. Additionally, the non-linear analysis using the PLFC model demonstrates that CLF has a stronger negative impact on LOGEU under conditions of high LOGPGDP.

The findings obtained through the POLS method show that while LOGPGDP tends to increase LOGEU, GEF contributes to its reduction in Europe. To address LOGEU in Europe, the role of CLF is essential. Specifically, CLF refers to investment expenditures on technologies related to energy saving and the implementation of renewable energy. Advancing technologies aimed at energy efficiency and clean energy transition is important for all economic sectors, including households, businesses, and government entities. However, the costs associated with these technologies and equipment are often high. Therefore, government support in the form of subsidies, tax preferences, and low-interest credits for the purchase of energy-saving and clean energy technologies is critical.

Furthermore, the stage of LOGPGDP plays a significant role in climate investment. European nations should maintain certain levels of LOGPGDP to achieve a substantial effect of CLF on reducing LOGEU.